堆

堆是一颗完全二叉树，小根堆的每一个节点的值都小于他的子节点的值

存储

可以使用一维数组来存储堆，注意下标从一开始

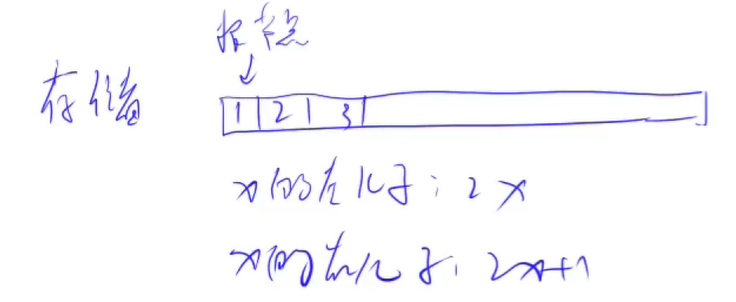
这里就有两种基础操作：

1. down() 当一个数变大时，down(k)是将这个节点向下沉
2. up() 当一个数变小时，up(k)是将这个节点向上浮

操作

通过数组模拟小根堆可以实现的操作：

1. 插入一个数

heap(++size)=x;
up(size);

2. 求集合中的最小值

heap[1];

3. 删除最小值

heap[1]=heap[size--];
down(1);

4. 删除任意元素

heap[k]=heap[size--];
// 这两种操作只会进行一个
down(k);
up(k);

5. 修改任意元素

heap[k]=x;
down(k);
up(k);

STL优先队列支持前三种操作

题目

堆排序

#include <iostream>
#include <algorithm>
using namespace std;

const int N=1e5+10;

int h[N],s;

// 这里没有用到
void up(int x)
{
    while(x/2&&h[x/2]>h[x]) 
    {
        swap(h[x],h[x/2]);
        x/=2;
    }
}


void down(int x)
{
    int u=x;
    if(x*2<=s&&h[u]>h[x*2]) u=x*2;
    if((x*2+1)<=s&&h[u]>h[x*2+1]) u=x*2+1;
    if(u!=x)
    {
        swap(h[x],h[u]);
        down(x);
    }
}

int main()
{
    int m,n;
    cin>>m>>n;
    s=m;
    for(int i=1;i<=m;i++) cin>>h[i];
    for(int i=m/2;i>0;i--) down(i);
    while(n--)
    {
        cout<<h[1]<<" ";
        h[1]=h[s--];
        down(1);
    }
    return 0;
}

哈希表

假定由1e5个数，分布在-1e9到1e9的区间中，这样是很难操作的，想要把他每一个数映射到一个0-1e5的区间中，这时就要用到哈希 最容易想到的方法就是x%1e5，但是这样肯定会有冲突产生，比如1e5+1和2e5+1，所以需要特殊的存储结构来尽可能的减少冲突

模拟散列表

开放寻址法

只需要开一个二到三倍的一维数组，每次哈希后，判断当前位置是否已经被占用，如果是就向后继续看，看到末尾再回头看继续看

#include <iostream>
#include <cstring>
using namespace std;


// 开放寻址法数组大小开2至3倍
const int N=200003,null=0x3f3f3f3f;

int h[N];


int find(int x)
{
    int k=(x%N+N)%N;
    while(h[k]!=null&&h[k]!=x)
    {
        k++;
        if(k==N) k=0;
    }
    return k;
}

int main()
{
    memset(h, null, sizeof h);
    int n;
    cin>>n;
    
    while(n--)
    {
        char op;
        int x;
        cin>>op>>x;
        int k=find(x);
        if(op=='I') h[k]=x;
        else
        {
            if(h[k]!=null) cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
    }
    
    return 0;
}

拉链法

开一个一维数组，将每一个元素都当成链表的头指针，即

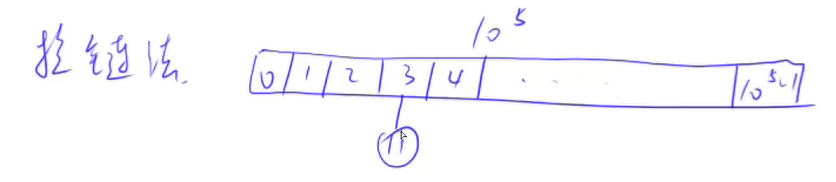
#include <iostream>
#include <cstring>
using namespace std;


// 一般取模的数是质数并且远离2的n次幂，冲突的概率会降低
const int N=100003;
int h[N],e[N],ne[N],idx;


void insert(int x)
{
    // 这样可以保证负数的结果也可以落在0-1e5区间内
    int k=((x%N)+N)%N;
    e[idx]=x;
    ne[idx]=h[k];
    h[k]=idx++;
}

bool find(int x)
{
    int k=((x%N)+N)%N;
    for(int i=h[k];i!=-1;i=ne[i])
        if(e[i]==x) return true;
    return false;
}

int main()
{
    int n;
    cin>>n;
    // 初始化整个指针数组为-1
    memset(h, -1, sizeof h);
    while(n--)
    {
        char op;
        int x;
        cin>>op>>x;
        if(op=='I')
        {
            insert(x);
        }
        else
        {
            if(find(x)) cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
    }
    
    return 0;
}

字符串哈希

关于字符串的操作，还可以使用哈希来进行比较

假设有一个字符串只有小写字母"abc"，可以使用它的ASCII码值或从1开始编号，得123，由减少哈希冲突的经验我们取这个数为131进制,即(123)₁₃₁

我们将这个转换为10进制，数字有可能会非常大，所以会进行一次哈希，这里取N为2⁶⁴,因为这样我们可以很方便的将结果定义为 unsigned long long，我们就不用再去自己取余了，这样我们就得到了一个字符串的哈希值

字符串哈希

此题使用字符串哈希和前缀和

#include <bits/stdc++.h>                         //字符串前缀哈希
using namespace std;
typedef unsigned long long ull;//用ull省去取模的步骤

const int N=100010,P=131;//经验：进制p取131或13331

ull h[N],p[N];
char a[N];

ull get(int l,int r){
    // 由于将字符串变成了数字，有了维权的影响处于高位的abc和低位的abc哈希值是不同的，所以要用p数组记录位权，才能正常比较
    return h[r]-h[l-1]*p[r-l+1];          //h是哈希前缀和数组
}

int main(){
    int m,n;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];       //注意要从1开始
    p[0]=1;                                 //注意p【0】要赋值为一
    for(int i=1;i<=n;i++){
        h[i]=h[i-1]*P+a[i];          //求哈希前缀和数组，a【i】用的是ascii码表
        p[i]=p[i-1]*P;                       //记录位权大小
    }
    while(m--){
        int l1,l2,r1,r2;
        cin>>l1>>r1>>l2>>r2;
        if(get(l1,r1)==get(l2,r2)) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}