本章讲解dp中的经典题目背包问题。dp问题更像是数学问题,关键在于找到状态转移方程。
01背包
01背包是指给定n个物品,给出它们的体积和价值,在容量为m的背包下,能放下的最大价值是多少?
朴素
这里我们使用闫式dp法,有以下图解:
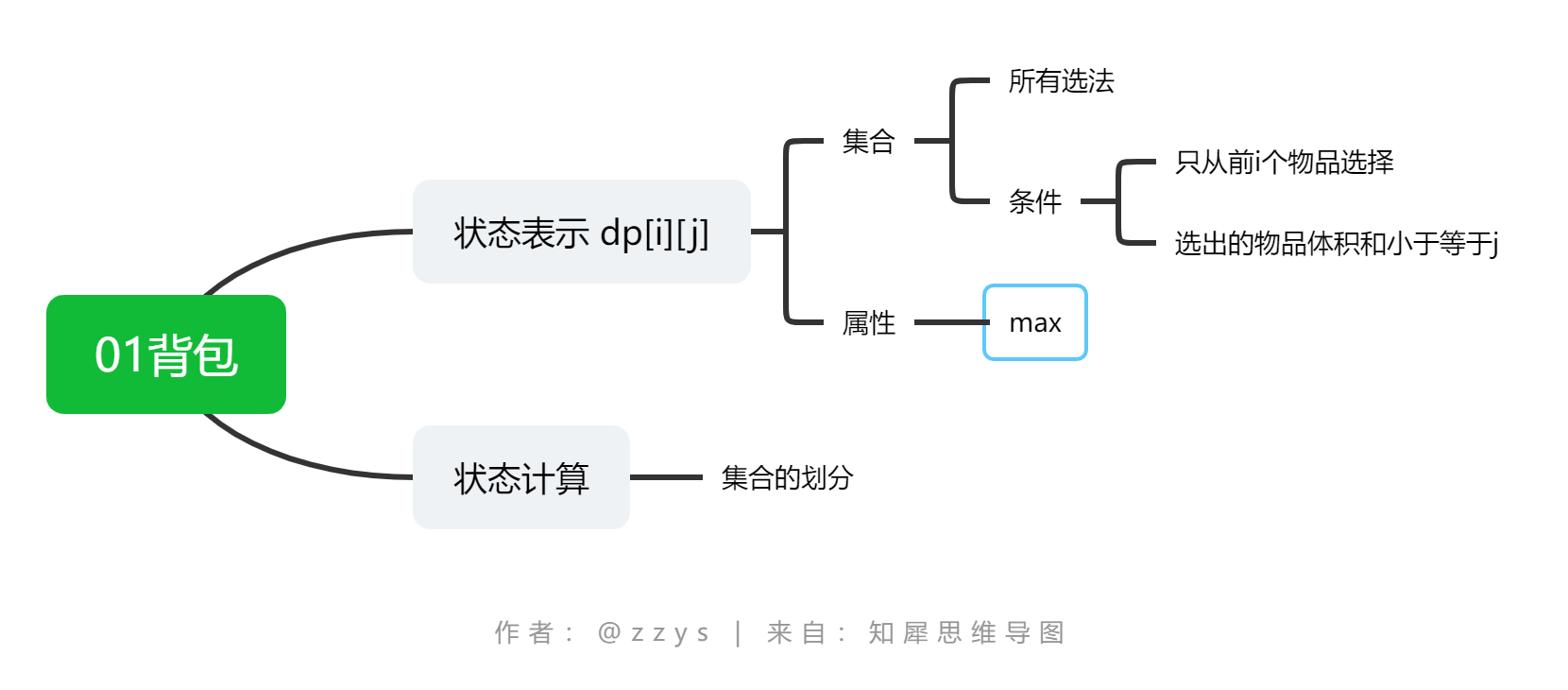
对于集合的划分,有以下图:

我们在计算dp[i][j]时,可以先计算dp[i - 1][j],即先计算只选前i - 1个物品,容量大小为j的情况,再和dp[i][j]取最大值,而dp[i - 1][j]又可以进一步向更小的范围减小,直到缩小到我们可以直接得到答案的范围。
目前的问题就是如何计算dp[i][j],有以下曲线救国的方法,直接求不好求,我们同样可以转换到i - 1层,有以下等式:dp[i][j] = dp[i - 1][j - v[i]] + w[i]。这里v存放的是体积,w存放的是价值。
所以综合看来有以下状态转移方程:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])。
那么就有以下代码:
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;
using namespace std;
const int N = 1e3 + 10;
int n,m;
int dp[N][N];
int v[N], w[N];
int main()
{
cin >> n >> m;
rep(i,1,n) cin >> v[i] >> w[i];
rep(i,1,n)
rep(j,1,m)
{
dp[i][j] = dp[i - 1][j];
if(j >= v[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
cout << dp[n][m];
return 0;
}
优化
dp问题通常可以优化,优化的方式通常是状态转移方程的等价变形,降低dp的维数。在本题中,可以发现
dp[i]层的状态只从dp[i - 1]层中获取- 用于更新
dp[i][j]的第二维状态,是永远小于j的。
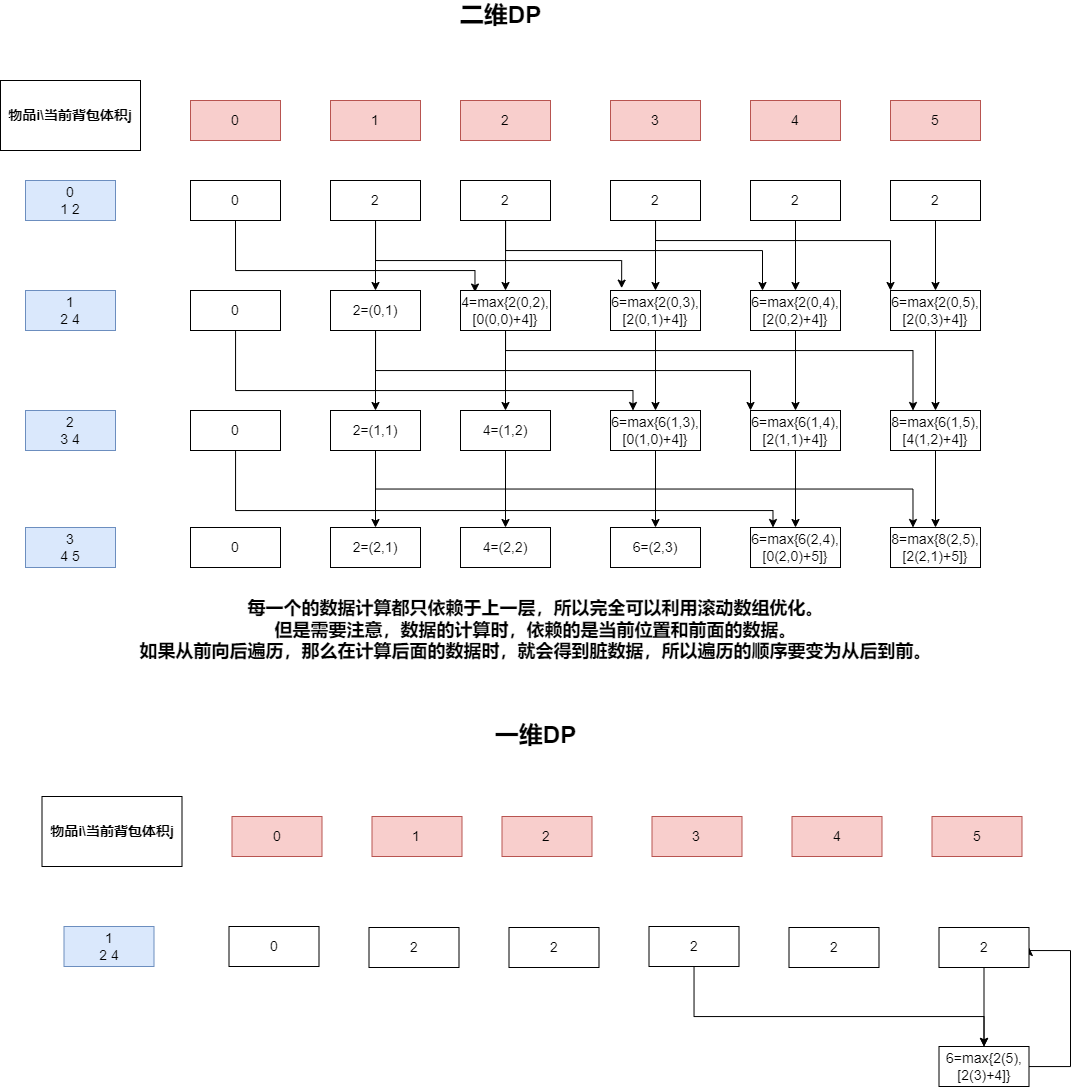
那么就可以使用滚动数组来进行优化,同时注意这里需要对第二层循环进行倒序遍历,因为我们知道我们用于更新dp[i][j]的状态是小于j的,如果我们先更新了较小的j,那么较大的j所使用的状态就已经被污染,不再是dp[i - 1][j]而是dp[i][j]。
以下是优化为一维dp后的代码
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i >= (l); -- i)
typedef long long LL;
using namespace std;
const int N = 1e3 + 10;
int n,m;
int dp[N];
int v[N], w[N];
int main()
{
cin >> n >> m;
rep(i,1,n) cin >> v[i] >> w[i];
rep(i,1,n)
per(j,m,v[i])
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
cout << dp[m];
return 0;
}
完全背包
在01背包问题的基础上,每一个物品可以无限制的选择。
朴素
同样使用闫式dp法,dp分析图和01背包相同。集合划分如下:

我们将集合划分为不选第i个物品,选1个第i个物品,....,选k个第i个物品。
有转移方程: dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]),注意不选第i个物品即k等于0的情况,所以不需要单独讨论。
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
using namespace std;
const int N = 1e3 + 10;
int n, m;
int v[N], w[N];
int dp[N][N];
int main()
{
cin >> n >> m;
rep(i, 1, n) cin >> v[i] >> w[i];
rep(i, 1, n)
rep(j, 0, m)
for(int k = 0; k * v[i] <= j; k++)
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
cout << dp[n][m];
return 0;
}
优化
可以考虑如下式子:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v]+w,dp[i-1][j-2v]+2w,dp[i-1][j-2v]+3w,...)
dp[i][j-v]=max( dp[i-1][j-v]),dp[i-1][j-2v]+w,dp[i-1][j-2v]+2w...)
--->
dp[i][j]=max(dp[i-1][j],dp[i][j-v]+w);
简化后的式子可以减少的重复状态的计算,直接使用同一层前面的状态来更新当前状态。
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
using namespace std;
typedef pair<int, int> PII;
const int N = 1e3 + 10;
int n, m;
int v[N], w[N];
int dp[N][N];
int main()
{
cin >> n >> m;
rep(i, 1, n) cin >> v[i] >> w[i];
rep(i, 1, n)
rep(j, 0, m)
{
dp[i][j] = dp[i - 1][j];
if(v[i] <= j) dp[i][j]=max(dp[i][j],dp[i][j - v[i]] + w[i]);
}
cout << dp[n][m];
return 0;
}
然后会发现当前情况仅仅使用了i-1和i层的状态,又可以使用滚动数组进行优化,不同的是,我们在更新时,使用的是本层的状态,也就是dp[i][j]使用的是dp[i][j - v]的状态,所以要先更新前面的状态再更新当前状态。
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i >= (l); -- i)
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
typedef pair<int, int> PII;
const int N = 1e3 + 10;
int n, m;
int v[N], w[N];
int dp[N];
int main()
{
cin >> n >> m;
rep(i, 1, n) cin >> v[i] >> w[i];
rep(i, 1, n)
rep(j,v[i],m)
dp[j]=max(dp[j],dp[j - v[i]] + w[i]);
cout << dp[m];
return 0;
}
多重背包
在完全背包的基础上,将每个物品的个数做了限制。
朴素
可以直接使用朴素版完全背包的代码,在枚举个数时加上限制
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i >= (l); -- i)
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
typedef pair<int, int> PII;
const int N = 1e3 + 10;
int v[N], w[N], s[N];
int dp[N][N];
int main()
{
int n, m;
cin >> n >> m;
rep(i, 1, n) cin >> v[i] >> w[i] >> s[i];
rep(i, 1, n)
rep(j, 0, m)
for(int k = 0; k * v[i] <= j && k <= s[i]; k++)
dp[i][j] = max(dp[i][j],dp[i - 1][j - v[i] * k] + k * w[i]);
cout << dp[n][m];
return 0;
}
优化
注意,在这道题中,我们不能使用完全背包的优化方式,因为它给了每个物品的个数限制,所以上个等式会有以下改变
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v]+w,...,dp[i-1][j-s*v]+s*w)
dp[i][j-v]=max( dp[i-1][j-v]) ,...,dp[i-1][j-s*v]+(s-1)*w,dp[i-1][j-(s+1)*v]+s*w)
我们可以发现第二个式子,最后多出一项,我们无法获取两个式子之间最大值的关系,所以这个方法不可行。
这里考虑使用二进制优化,举个例子:对于给定的物品i,有它的数量20,那么我们可以使用二进制来表示总体的数量,将20转换为1+2+4+8+5,我们可以通过这五个数的任意搭配来组成1-20的任意选法。最后分好组后,使用01背包问题,进行选择即可。
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i >= (l); -- i)
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
int v[N],w[N];
int dp[N];
int main()
{
int n, m;
cin >> n >> m;
int cnt = 0;
rep(i, 1, n)
{
int k = 1;
int a, b, s;
cin >> a >> b >> s;
while(k <= s)
{
cnt ++;
v[cnt] = k * a;
w[cnt] = k * b;
s -= k;
k *= 2;
}
if(s > 0)
{
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
rep(i, 1, n)
per(j, m, v[i])
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
cout << dp[m];
return 0;
}
分组背包
在01背包的基础上,给定几个组别,每个组别内东西的选择是互斥的。
这个问题和多重背包问题相似,只不过多重背包问题的集合划分是根据选几个来分,而这道题是根据在一组内选哪个来分。
#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i >= (l); -- i)
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
typedef pair<int, int> PII;
const int N=110;
int dp[N],w[N][N],v[N][N],s[N];
int main(){
int m,n;
cin >> n >> m;
rep(i, 1, n)
{
cin >> s[i];
rep(j, 1, s[i])
cin >> v[i][j] >> w[i][j];
}
rep(i, 1, n)
per(j, m, 0)
rep(k, 1, s[i])
if (v[i][k] <= j)
dp[j] = max(dp[j], dp[j - v[i][k]] + w[i][k]);
cout << dp[m];
return 0;
}