有关图的算法，包括最短路，最小生成树，二分图

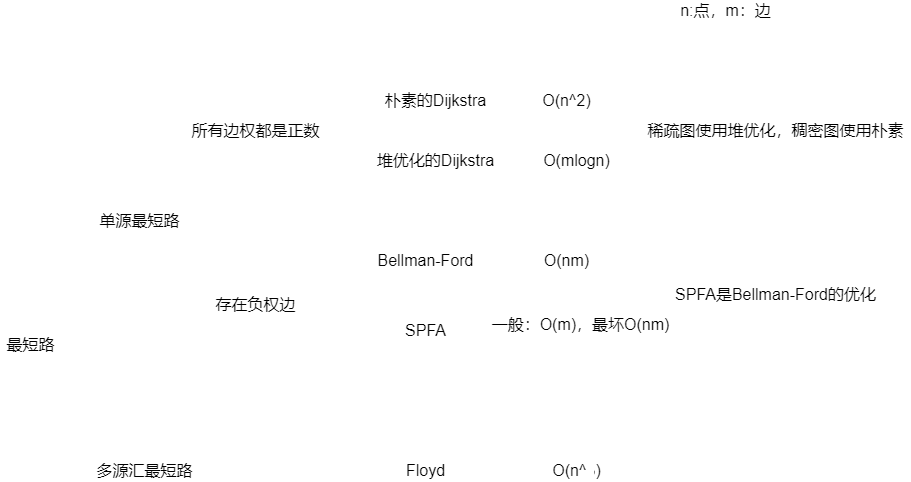
最短路.drawio.png

最短路

1. 单源最短路

1.1 Dijkstra算法

对于没有负权边的单源最短路问题，通常使用Dijkstra算法解决，其中当图是稀疏图时，考虑使用堆优化版的Dijkstra算法，稠密图使用朴素版的Dijkstra算法

1.1.1 朴素版的Dijkstra算法

初始化起点为0，其他点为正无穷，定义s数组为已经确定最短路的点
循环n次，每次选取不在集合s中，距离起点最近的点t，加入集合s中，更新其他点的最短路径

常用模板：

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i < (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
const int N = 1e3 + 10;
int n, m;
int g[N][N], dist[N];
bool st[N];

int Dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    // 初始化第一个点的距离为0
    dist[1] = 0;
    
    rep(i,1,n + 1)
    {
        // st[]中为true的点的集合，就是已经确定最短距离的集合s
        // 借助t从而选取不在s中，且距离最小的一个点加入s中
        // 注意这里是以假设图中没有负权边为前提
        int t = -1;
        rep(j,1,n + 1)
            if(!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
        
        // 将该点加入s中
        st[t] = true;
        
        if(t == n) break;
        
        // 更新其他点的最短路径
        rep(j,1,n + 1)
            dist[j] = min(dist[t] + g[t][j], dist[j]);
        
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    memset(g,0x3f,sizeof g);
    cin >> n >> m;
    
    rep(i,1,m + 1)
    {
        int a, b, c;
        cin >> a >> b >> c;
        // 处理重边
        g[a][b] = min(g[a][b], c);
    }
    
    cout << Dijkstra();
    
    return 0;
}

1.1.2 堆优化的Dijkstra算法

朴素版中最耗时的操作是以下两步
1. 在未确定最短距离的集合中寻找最小值
2. 用新选出的点更新其他的边
无论图是稠密图还是稀疏图，都要遍历n边，但是可以考虑一下稀疏图，他的出边实际上并没有n那么多，所以首先可以考虑使用邻接表来存储，这样遍历更新的次数会减少
对于寻找最小值，可以考虑使用优先队列来进行维护寻找

由于对于一个点，队列不支持原地修改，所以可能在队列中存在多个边，所以要使用st数组维护状态

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i < (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
typedef pair<int,int> PII;
const int N = 1e6 + 10;
int n, m;
int e[N], ne[N], w[N], h[N], dist[N], idx;
bool st[N];


void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++; 
}

int Dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    // 初始化第一个点的距离为0
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    
    heap.push({0,1});
    
    
    while(heap.size())
    {
        auto t = heap.top();
        int dis = t.first , ver = t.second;
        heap.pop();
        if(st[ver]) continue;
        st[ver] = true;
        
        for(int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dis + w[i])
            {
                dist[j] = dis + w[i];
                heap.push({dist[j],j});
            }
            
        }
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    memset(h,-1,sizeof h);
    cin >> n >> m;
    
    rep(i,1,m + 1)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a,b,c);
    }
    
    cout << Dijkstra();
    
    return 0;
}

1.2 Bellman-Ford算法

当存在负权边时，不能使用Dijsktra算法，选择采用Bellman-Ford算法。

这个算法的思想是：循环n遍，循环内部遍历m条边（a,b,w），计算dist[b] = min(dist[b],dist[a] + w)。其中n的含义是，最多经过n条边选取的最短路径。

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
typedef pair<int,int> PII;
const int N = 1e4;
const int M = 1e5 + 10;
int n, m, k, idx;
int dist[N],backup[N];
int e[N], ne[N], h[N], w[N];

int add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void bf()
{
    memset(dist, 0x3f, sizeof dist);
 
    dist[1] = 0;
    
    rep(i, 1, k)
    {
        memcpy(backup, dist, sizeof dist);
        rep(i, 1, n)
        {
            for(int j = h[i]; j != -1; j = ne[j])
            {
                int t = e[j];
                //  注意使用备份数组防止串联修改
                dist[t] = min(dist[t], backup[i] + w[j]);
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    
    cin >> n >> m >> k;
    
    rep(i, 1, m)
    {
        int x, y, z;
        cin >> x >> y >> z;
        add(x,y,z);
    }
    bf();
    if (dist[n] > 0x3f3f3f3f / 2) cout << "impossible";
    else cout << dist[n];
    
    return 0;
}

backup数组的含义：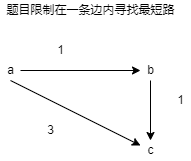

如果不使用backup：在第一次遍历，也是唯一一次遍历时：原本b的距离是正无穷，c的距离也是正无穷，在遍历所有边时，先将b更新为1，再更新c时，就会将b更新为2，但这很显然超出了预期。
如果使用backup，每一次更新都使用backup的数据，虽然先将b更新为1，但是backup中b的距离依然是正无穷，这样就符合我们的预期。

对于这个判断条件dist[n] > 0x3f3f3f3f / 2，是因为对于n和n-1两个点，如果起点无法到达，那么它们两个的dist就是正无穷，但是一旦这两个之间的距离为负数，就有可能将n的dist更新的比0x3f3f3f3f要小，所以就去一个保险值。

1.3 SPFA算法

SPFA是bellman-frod算法的改进版，可以发现，dist[t] = min(dist[t], backup[i] + w[j]);这一步并不是每一次都真的进行更新操作，只有在i点的距离发生变小后，才会更新t的距离。

所以可以采用宽搜的思想，当我们将一个点的距离更新后，就将其放入队列中，更新它的所有出边。当队列为空时，也就没有可以更新的点了。

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
typedef pair<int,int> PII;
const int N = 1e5 + 10;
int e[N], ne[N], h[N], w[N];
int n, m, idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(dist,0x3f,sizeof dist);
    
    dist[1] = 0;
    
    queue<int> q;
    q.push(1);
    st[1] = true;
    while(q.size())
    {
        int t = q.front();
        st[t] = false;
        q.pop();
        
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    
    rep(i, 1, m)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    spfa();
    if(dist[n] == 0x3f3f3f3f) cout << "impossible";
    else cout << dist[n];
    return 0;
}

可以利用SPFA来求图中是否存在负环：每当一条边更新一遍时，它所经历的边数就是更新它的点的边数加一，如果这个数字大于等于点数，那么就存在一个环，由于此算法是求最短路，所以该环就是负环。

注意负环有可能从起点无法到达，所以将所有点都放入SPFA中进行计算

#include <bits/stdc++.h>//spfa求负环 
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N=1e6;
int n,m;
int d[N],h[N],e[N],ne[N],w[N],idx,cnt[N];
bool st[N];

void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

bool spfa()
{
    queue<int> a;
    for(int i=1;i<=n;i++)//将所有点入队
    {
        a.push(i);
        st[i]=true;
    }
    while(a.size())
    {
        int t=a.front();
        a.pop();
        st[t]=false;
        
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                cnt[j]=cnt[t]+1;//每次成功更新，都让其经过的边数等于与上一个点加一，
                if(cnt[j]>=n) return true;//如果说经过的变数大于总点数 ，那么一定有重复点，也就是存在环
                if(!st[j])
                {
                    st[j]=true;
                    a.push(j);
                }
            }
        }
    };
    return false
}

int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    if(spfa()) cout<<"Yes";
    else cout<<"No";
    return 0;
}

2. 多源最短路

2.1 Floyd算法

Floyd基于动态规划，用于求解多源最短路

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
const int N=3e2;
const int INF = 1e9;
int n, m, k;
int g[N][N];


void floyd()
{
    rep(k, 1, n)
        rep(i, 1, n)
            rep(j, 1, n)
                g[i][j] = min(g[i][j] , g[i][k] + g[k][j]);
}

int main()
{
    cin >> n >> m >> k;
    
    rep(i,1,n)
    {
        rep(j, 1, n)
        {
            if (i == j) g[i][j] = 0;
            else g[i][j] = INF;
        }
    }
    rep(i, 1, m)
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);
    }
    floyd();
    
    while(k --)
    {
        int a, b;
        cin >> a >> b;
        if (g[a][b] > INF / 2) cout << "impossible" << endl;
        else cout << g[a][b] << endl;
    }
    
    return 0;
}

最小生成树

一般来说稠密图使用朴素版的prim算法，稀疏图堆优化版的prim算法和Kruskal算法都可以用，由于Kruskal较短，所以优先使用Kruskal。

1. prim 算法

1.1.1 朴素版prim算法

时间复杂度：O(n^2)

和Dijkstra思路相似，只不过dist数组维护的是点到集合的最短距离

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
typedef pair<int,int> PII;
const int N = 510;
const int INF = 0x3f3f3f3f;
int n, m;
int g[N][N],dist[N];
bool st[N];

int prim()
{
    int ans = 0;
    memset(dist,INF,sizeof dist);
    dist[1] = 0;
    rep(i, 1, n)
    {
        int t = -1;
        rep(j, 1, n)
            if (!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
            
        if (dist[t] == INF) return INF;
        ans += dist[t];
        st[t] = true;
        
        rep(j,1,n)
            dist[j] = min(dist[j] ,g[t][j]);
    }
    return ans;
}


int main()
{
    memset(g,INF,sizeof g);
    cin >> n >> m;
    while (m -- )
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
    }
    int t = prim();
    if (t == INF) cout <<"impossible" << endl;
    else cout << t << endl;
    
    return 0;
}

1.1.2 堆优化版prim算法

时间复杂度：O(mlogn)

2. Kruskal 算法

时间复杂度：O(mlogm)

将所有边按权重从小到大排序（快速排序）
枚举每条边a，b 权重c。如果a，b不连通，将这条边加入集合中（并查集维护）

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
typedef pair<int,int> PII;
const int M = 2e5 + 10;
int n, m;
int p[M];
struct Edge
{
    int a, b, w;
}edge[M];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}
bool cmp(Edge a, Edge b)
{
    return a.w < b.w;
}
int main()
{
    cin >> n >> m;
    rep(i, 1, n) p[i] = i;
    rep(i, 1, m)
    {
        int a, b, c;
        cin >> a >> b >> c;
        edge[i] = {a, b, c};
    }
    
    sort(edge + 1, edge + m + 1, cmp);
    int res = 0, cnt = 0;
    
    rep(i, 1, m)
    {
        int a = edge[i].a, b = edge[i].b, w = edge[i].w;
        a = find(a), b = find(b);
        if(a != b)
        {
            p[a] = b;
            res += w;
            cnt ++;
        }
    }
    if (cnt < n - 1) cout << "impossible" << endl;
    else cout << res;
    return 0;
}

二分图

一个图是二分图当且仅当图中不含奇数环（边数）

1. 染色法

时间复杂度：O(n+m)

染色法用来判断一个图是否是二分图，从起点开始，将起点染成1，然后把所有相邻的点染成2，依次类推，如果发现有相邻的点颜色相同，那么就说明存在奇数环，不是二分图。

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
typedef pair<int,int> PII;
const int N = 2e5 + 10;
int n, m;
int e[N], ne[N], h[N], idx;
int c[N];
void add(int a, int b)
{
    e[idx] = b,  ne[idx] = h[a] , h[a] = idx ++;
}


bool dfs(int u, int color)
{
    c[u] = color;
    
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        
        if(!c[j])
        {
            if(!dfs(j,3 - color)) return false;
        }
        else if(c[j] == color) return false;
    }
    return true;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    rep(i, 1, m)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    bool f = true;
    rep(i, 1, n)
    {
        if (!c[i])
        {
            if (!dfs(i,1))
            {
                f = false;
                break;
            }
        }
    }
    if (!f) cout << "No";
    else cout << "Yes";
    return 0;
}

2. 匈牙利算法

时间复杂度：O(mn)，但实际运行时间远小于O(mn)

使用匈牙利算法来求一个给定的二分图的最大匹配值。

对于给定的一个二分图，将左半边称为男孩团体，右半边乘坐女孩团体，解题目的就是能最大数量组成情侣。其中如果两个异性存在一条边，则看作有好感度，可以尝试组成情侣，否则不予考虑。

遍历男生团体，对于其中一个男生，我们遍历所有和他有好感度的女生：

当前女生还未匹配，则组成情侣
当前女生已经匹配，但是和她匹配的男生还可以找到新的女生（递归进行1，2）
遍历过了所有女生都无法匹配，则放弃

在代码中math数组用来维护男女的匹配情况。st数组用来维护在每一个男生寻找匹配时，女生被匹配的状态，保证递归寻找不要去寻找重复的匹配，否则会陷入死循环

#include <bits/stdc++.h>
#define rep(i,l,r) for (int i = (l); i <= (r); ++ i)
#define per(i,r,l) for (int i = (r); i > (l); -- i)
typedef long long LL;

using namespace  std;
typedef pair<int,int> PII;
const int N = 5e2 + 10;
const int M = 1e5 + 10;
int e[M], ne[M], h[N], idx;
int n1, n2, m;
bool st[N];
int math[N];

void add(int a, int b)
{
    e[idx] = b,  ne[idx] = h[a] , h[a] = idx ++;
}

bool find(int u)
{
    for(int i = h[u] ; i != -1; i = ne[i])
    {
        int j = e[i];
        
        if (!st[j])
        {
            st[j] = true;
            if (math[j] == 0 || find(math[j]))
            {
                math[j] = u;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    memset(h, -1, sizeof h);

    cin >> n1 >> n2 >> m;
    
    while (m -- )
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    int res = 0;
    rep(i,1,n1)
    {
        memset(st,false,sizeof st);
        if(find(i)) res ++;
    }
    cout << res;
    return 0;
}

# 最短路

# 1. 单源最短路

# 1.1 Dijkstra算法

# 1.1.1 朴素版的Dijkstra算法

# 1.1.2 堆优化的Dijkstra算法

# 1.2 Bellman-Ford算法

# 1.3 SPFA算法

# 2. 多源最短路

# 2.1 Floyd算法

# 最小生成树

# 1. prim 算法

# 1.1.1 朴素版prim算法

# 1.1.2 堆优化版prim算法

# 2. Kruskal 算法

# 二分图

# 1. 染色法

# 2. 匈牙利算法

最短路