这道题是一道简单题，但是在写的过程中发现了一些知识的盲点以及新颖的做法，所以记录一下：x 的平方根

二分

第一种做法就是简单的小数二分，按照记忆中的模板测试一下：

int mySqrt(int x) {
    double l = 1, r = x / 2;
    while(r - l > 1e-8) {
        double mid = l + (r - l) / 2;
        if(mid < x / mid) l = mid;
        else r = mid;
    }
    printf("%.6lf", l);
    return l;
}

发现竟然错了一个4，奇怪的是打印的是2.000000，返回的却是1。

这里卡了我很久，后面将.6f改为.8f后发现打印的是1.99999999，即原来的打印是经过四舍五入的，让我以为是2.0，但实际上把小数去掉后确实应该是1。于是我在最后返回时加入了循环的精度。并且要对0特判一下就过了。

int mySqrt(int x) {
    if(x == 0) return 0;
    double l = 1, r = x / 2;
    while(r - l > 1e-8) {
        double mid = l + (r - l) / 2;
        if(mid < x / mid) l = mid;
        else r = mid;
    }
    printf("%.16lf", l + 1e-8);
    return l + 1e-8;
}

牛顿迭代法

利用导数，不断的逼近正确答案，具体的见图：

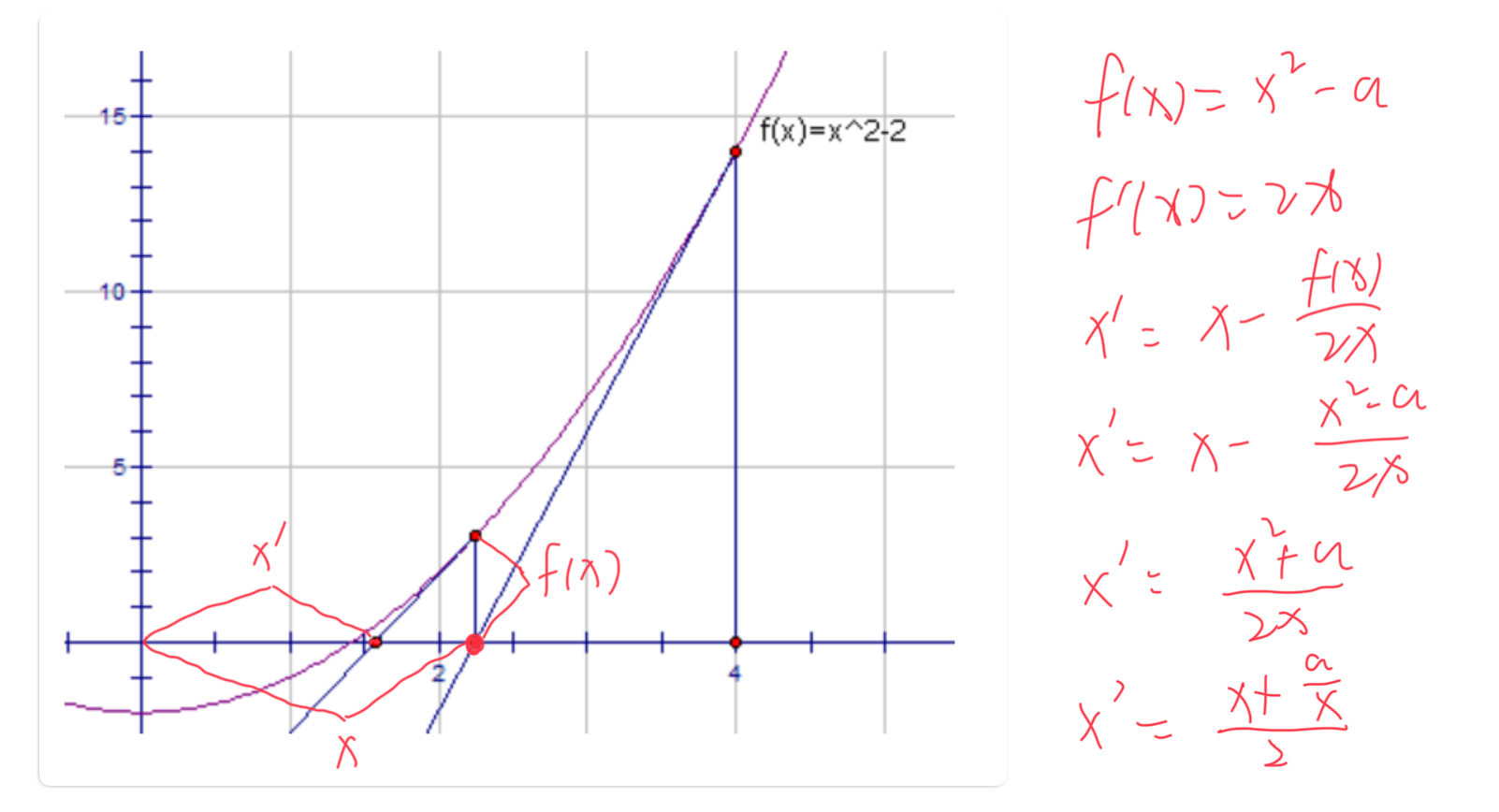
x'就是我们每一次逼近的结果。

int mySqrt(int x) {
    double old = x + 1.0;
    double better;
    while(1) {
        better = (old + x / old) / 2;
        if(abs(better - old) < 0.1) break;
        old = better;    
    }
    return better;
}

old起始一定要加1.0，对于x = 1来说better = (old + x / old) / 2;只会给better赋值为1。而对于 x == 2来说，会发生除零错误。